신경망 학습은 저번 시간에 학습했던 신경망에서, 어떤식으로 학습을 하는지에 대한 이론이다.
학습
- 훈련 데이터로부터 가중치의 최적값을 자동으로 획득하는 것
학습의 목표
- 손실 함수의 결과값을 가장 작게 만드는 가중치를 찾는 것
- 손실 함수 : 신경명이 학습할 수 있도록 해주는 지표
신경망 학습에서는 손실 함수 라는 것을 사용한다.
일반적인 패턴을 찾고 손실 함수를 사용해 오차 범위를 줄여 정답을 찾아가는 과정이라고 보겠다.
왜 손실 함수를 사용하는거? 하면, 가중치의 값을 조금만 변화 시켜도 손실 함수의 값이 크게 변하기 때문에, 변화를 쉽게 감지할 수 있고, 가중치를 어떻게 조절해야할지 알 수 있다.
손실 함수
- 회귀 문제 : MSE (Mean squared error)
- 분류 문제 : Cross-Entropy
학습을 위해선 미니배치 학습이라고 하는 방식을 사용하는데, 훈련 데이터 일부를 골라 전체의 근사치로 사용한다.
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
y_batch = y_train[batch_mask]
코드 상에선 이렇게 batch_size 를 두어, 훈련 데이터 셋에서 무작위 10개를 골라내도록 구현한다.
손실 함수의 기울기를 통해 학습이 되는지 확인을 할 수 있다고 하는데, 그러기 위해선 수치 미분에 대한 개념을 알아야한다.
미분
- 변수 x 값의 변화량에 관한 함숫값 f(x)의 변화량 비
- x의 '작은 변화'가 함수 f(x)를 얼마나 변화시키는가
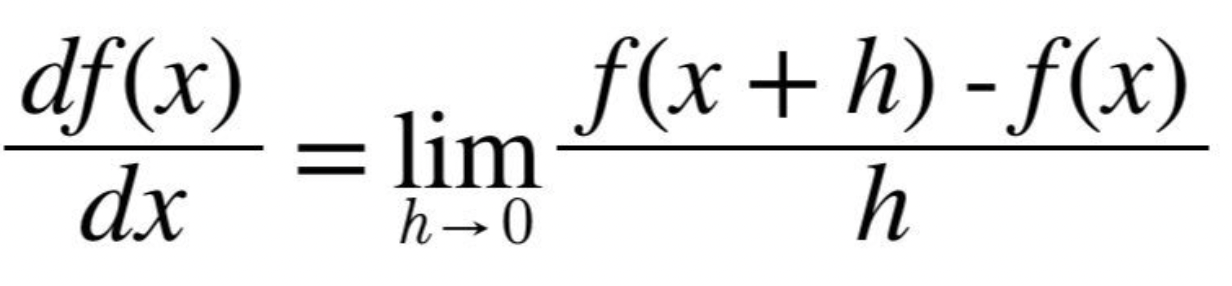
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def num_diff(f, x):
h = 1e-4 # 너무 작은 값을 사용하면 컴퓨터에서 계산하지 못한다고 한다. : 1e-50
return (f(x + h) - f(x)) / h
def function_1(x):
return 0.01 * x ** 2 + 0.1 * x
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.plot(x, y)
plt.show()
num_diff( function_1, 5 ) # x=5일 때의 미분 값
num_diff( function_1, 10 ) # x=10일 때의 미분 값
y = 0.01x^2 + 0.1x 의 해석적 미분은 df(x)/dx = 0.02x + 0.1 이므로
- 0.02 * 5 + 0.1 = 0.2
- 0.02 * 10 + 0.1 = 0.3
- 오차가 매우 낮다.
편미분
- 파라미터가 2개인 함수
- 변수가 여럿인 함수에 대한 미분
- 목표 변수 하나에 초점을 맞추고 다른 변수는 값을 고정하는 방식으로 구현한다.

def function_temp1(x0):
return x0 * x0 + 4.0 ** 2
num_diff( function_temp1, 3.0 )
# 결과 : 6.000099999994291
def function_temp2(x1):
return 3.0 ** 2 + x1 * x1
num_diff( function_temp2, 4.0 )
# 결과 : 8.00009999998963
기울기
- 기울기는 모든 변수의 편미분으로 이루어진 벡터
def num_grad(f, x):
h = 1e-4
grad = np.zeros_like(x) # x와 형상이 같고 원소가 모두 0인 배열 생성
for idx in range(x.size):
# 기존 x 값을 보관
temp = x[idx]
# f(x+h) 계산
x[idx] = temp + h
fxh1 = f(x)
# f(x-h) 계산
x[idx] = temp - h
fxh2 = f(x)
# 그리고 기울기 계산
grad[idx] = (fxh1 - fxh2) / (2*h) # 중앙차분 방식을 사용한 계산
# 다시 x를 원래대로
x[idx] = temp
return grad
def function_2(x):
return np.sum(x ** 2)
print( num_grad( function_2, np.array([3.0, 4.0]) ) )
# 6 8
print( num_grad( function_2, np.array([0.0, 2.0]) ) )
# 0 4
print( num_grad( function_2, np.array([3.0, 0.0]) ) )
# 6 0
기울기 하강 (Gradient Descent) - 손실함수가 내려가는 방향으로 이동
- 신경망은 학습 단계에서 최적의 가중치를 찾아야 함
- 최적의 가중치 : 손실 함수가 minimum이 되는 가중치
- 가중치의 공간이 넓기 때문에 어디가 minimum 인지 알기 어려움
- Gradient decent : 기울기를 활용해서 함수의 minimum 을 찾는 것
- 기울기가 가리키는 곳에 항사 minumum 이 있다는 보장은 없음
- Global minimum : 가장 작은 값
- Local minimum : 국조석인 최솟값
- Saddle point : 어느 방향에서 maximum, 다른 방향에서는 minimum 이 되는 점
- Plateau : 평평한 곳, 학습이 진행되지 않음

η (eta) 는 갱신하는 양 : 학습률
- 한번의 학습으로 얼마나 갱신할 지 지정
- 0.01 이나 0.001 등 특정 값을 정하는데 너무 크거나 작으면 학습이 잘 안될 수 있음
def gd( f, init_x, lr=0.01, step_num=100 ):
# f : 최적화 하려는 함수
# init_x : 초기 값
# lr : 학습률
# step_num : 반복 횟수
x = init_x
for i in range(step_num):
grad = num_grad(f, x)
x -= lr * grad
plt.scatter(x[0], x[1])
return x
def function_2(x):
return x[0]**2 + x[1]**2
init_x = np.array([-3.0, 4.0])
plt.xlim(-5, 5)
plt.ylim(-5, 5)
result = gd( function_2, init_x=init_x, lr=0.1, step_num=100 )
print(result)
plt.show()
# [ -6.11110793e-10 8.14814391e-10]
학습률이 너무 큰 경우엔 발산하고, 너무 작으면 갱신이 되지 않는다.
Hyperparameter 는 사용자가 직접 수동으로 설정해주는 값이며, 여러 후보 값들을 시험하며 가장 잘 학습하는 값을 찾는 과정을 Hyperparameter Tuning 이라고 한다.
신경망에서의 기울기는 결국 가중치에 대한 손실함수의 기울기를 뜻한다.
그래서 신경망 학습의 절차를 정리해보면
1 단계 - 미니배치
2 단계 - 기울기 산출
3 단계 - 매개변수 갱신
4 단계 - 1~3 단계 반복
이런식으로 이루어진다.
이 방식을 SGD (Stochastic Gradient Descent) 라고 하며,
대부분의 딥러닝 프레임워크에서는 SGD 라는 함수를 제공한다고 한다.
생각보다 공부해야 될 것이 너무 많았다..
코드 중심은 정말로 다음 시간에..
'Dev > AI' 카테고리의 다른 글
| [리뷰] 랭체인으로 LLM 기반의 AI 서비스 개발하기 (0) | 2024.05.15 |
|---|---|
| [리뷰] 머신러닝 교과서: 파이토치 편 (0) | 2024.02.21 |
| [인공지능개론] 신경망(Neural network)에 대해서 (0) | 2022.04.18 |
| [인공지능개론] 퍼셉트론(Perceptron)에 대해서 (2) | 2022.04.11 |
| 파이썬으로 할 수 있는 것들. (0) | 2019.08.23 |

